公文の算数で異分母の足し算がスタートするのが
E31~
初めは通分のしやすい小さい数なのですが、
教材の番号が進むと、かなり大きな数の通分をしないといけませn。
例えば

数の感覚が高い子は大丈夫なのですが、
数の感覚がちょっと弱い子は、なかなか大変。
ちょっとしたコツでできるようになるので、宿題で困っていたら助けてあげてくださいね!
基本の考え方
例えば
「16と24」
の通分であれば
大きい方の数を
×2
×3
とやっていって
小さい方の段にあるかを探す
が基本です。

ヒント:何の段で割れるかな
「6と27」
の通分だと
27×2
27×3
が頭の中でできなくて、四苦八苦する子どもは多い!
そこで「何の段で割れるかな?」がヒントになります。
6と27
だと
両方とも3で割れる。
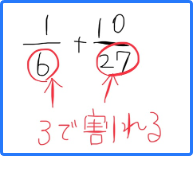
27÷3=9
この9を反対の数である6にかけます。
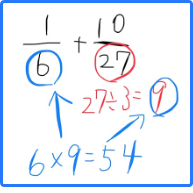
出てきた数が分母になる。
この場合54ですね。
「54で揃えてみて」のヒントで、子どもはできるようになります。

どうしても分からなかったら
どうしても分からなかったら・・・
割る数を書かせる

割った数を書かせる
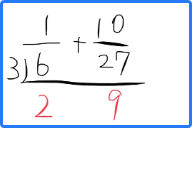
斜めにかけたら分母になる

上の数(分子)も、ななめにかけて出すことができます。

まとめ
分数計算は、高校数学につながる大切なポイントです。
ここでスラスラ解けるようにしておくことが必要!
最後の「書いて考える」は最後の手段。
できるだけ暗算で通分の数が見つけられるようになるまで
繰り返し練習をしましょう!
▼関連記事▼
公文の算数・数学は本当に役に立つ??子どもに実践させてきたママの意見







コメント